Category: Blog
Covertization- what is it?
Covertization sounds like an incredibly fancy concept that seems complicated. Although it comes in many forms, it is not difficult to explain what it is.
I first came across the word “Covertization” in Naveen’s blog about using it with the difference of two squares which can be found by using the following hyperlink: http://conceptionofthegood.co.uk/?p=777 . This concept really interested me and I wanted to know more so I decided to buy Engelmann’s Magnus Opus which is quite a large book if you did not already know!
Engelmann defines Covertization as “instruction that involves prompt shifts progressively from highly-prompted examples to unprompted examples”. The examples are given in the most simplest context to start with, and then the context changes, but the concept remains constant.
Naveen has taken this to mean a sequence of examples with explicit features transitioning to implicit features. This allows a process where students take small steps to go from each example that is presented. This means that the first example pupils encounter is structured within the simplest context.
I tried Covertization with simultaneous equations and getting students to realise when the two equations are in the form ready to be added or subtracted. As you can see from the picture below I have moved from a standard example where x can be eliminated to one where y is the subject of each equation. Going from one set of equations to another involves a small step that students can follow with ease. These examples allow students to see that x can be eliminated, y can be eliminated, the x and y terms may not always be lined up properly and they allow for deeper thinking into whether adding or subtracting is always the easiest way of eliminating a variable.
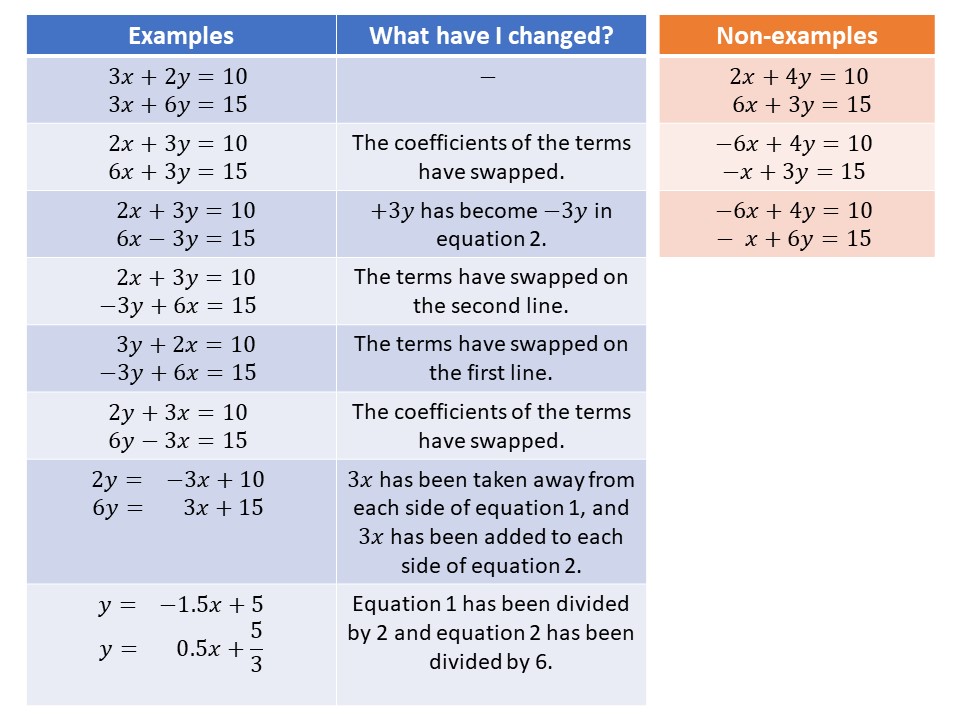
I do not use this type of covertization often because I believe that it is incredibly specific to certain topics. Naveen has used this process with the difference of two squares. I strongly advise you check her blog out! My most common use of covertization is “Dropping steps”. I call this “fading”. Many examples on this website are based on “fading”.
DBRS Process for Changing the subject of a formula
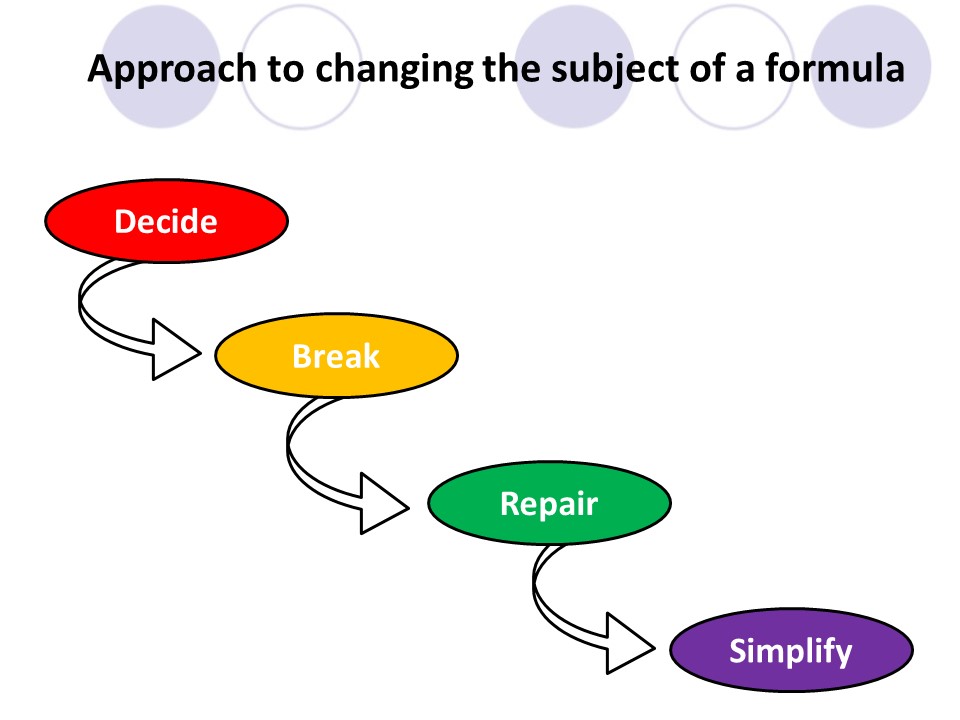
I promised I would post this! I have now presented about the process of Decide, Break, Repair and Simplify at Bristol and Sheffield maths conferences for changing the subject of a formula. This has been a pleasure and has been received incredibly well by a lot of maths teachers across the country.
The main idea of these workshops were to show how Kris Boulton’s method of solving linear equations can be adjusted to changing the subject of a formula.
The key difference for changing the subject of a formula when compared to linear equations is when we have to factorise… this can be a little daunting for students to do during a question as they normally get it wrong! However, during my presentation I mentioned how I have got around this problem with slides like below:
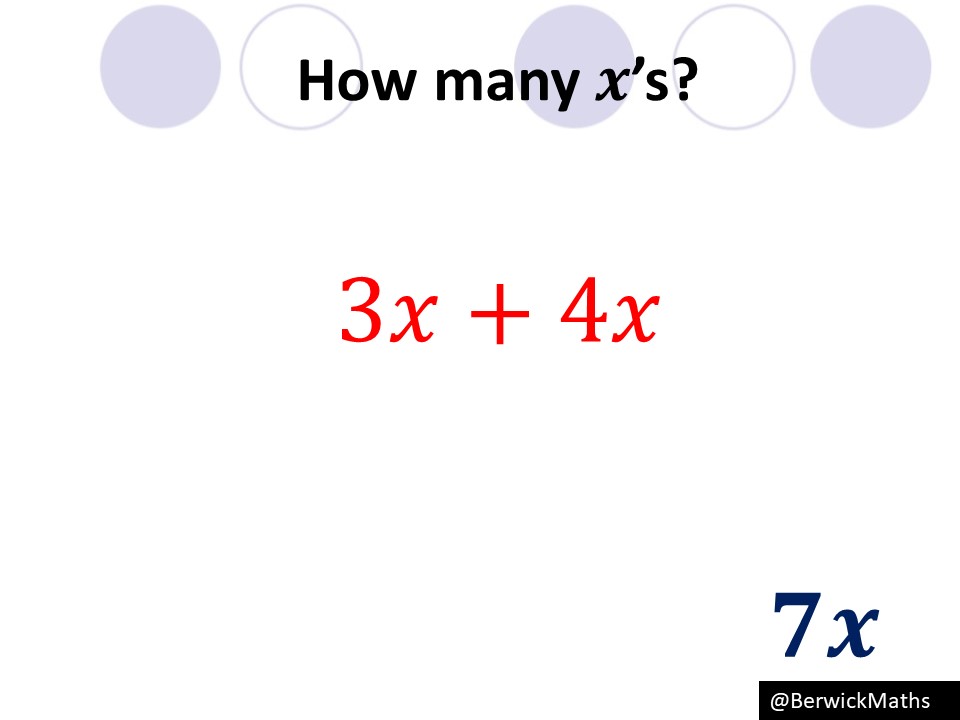
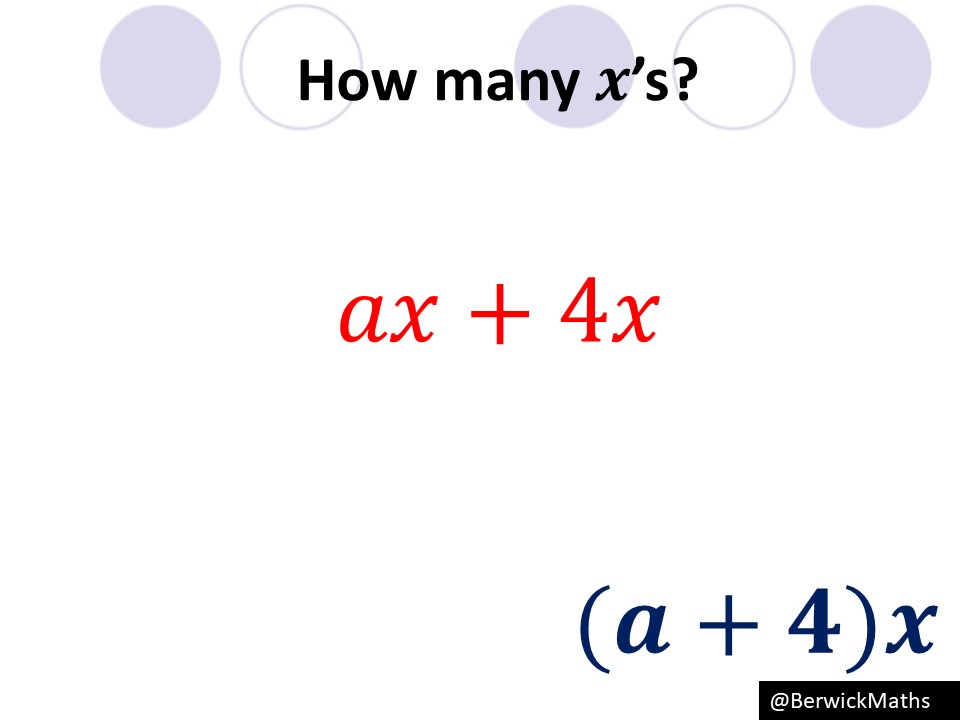
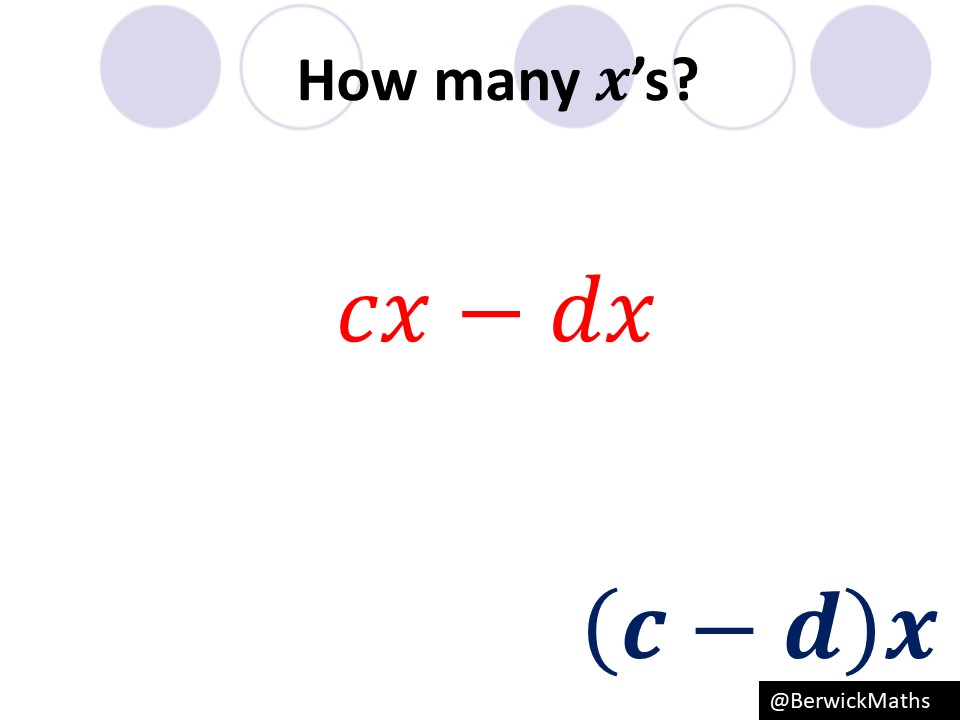
I have uploaded my powerpoint below! Please check it out!
The Decide, Break, Repair and Simplify process for linear equations (DBRS)
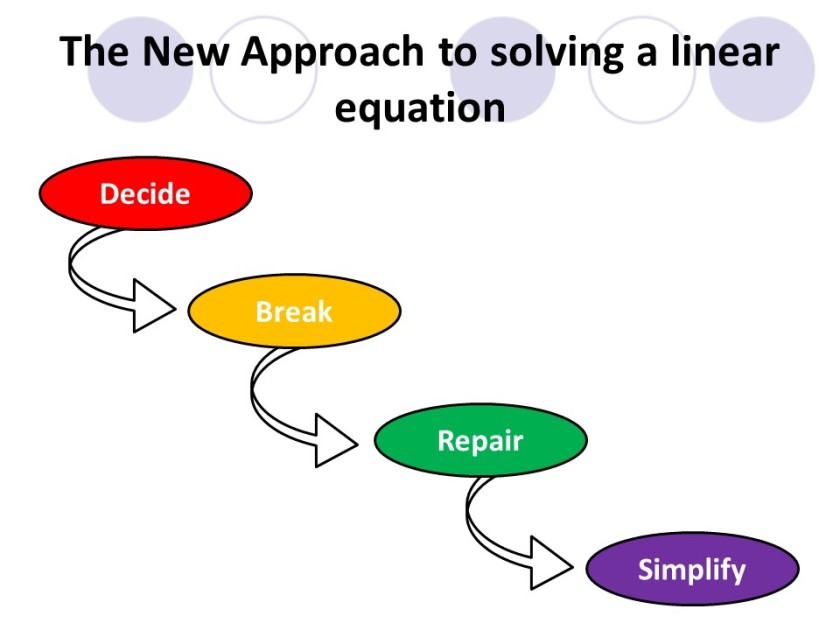
The Decide, Break, Repair and Simplify process was first introduced by Kris Boulton at the Birmingham maths conference in October 2018. The process is used to solve linear equations. I have adjusted it to rearranging the subject of a formula, but will not be posting this until I have presented it again at Sheffield. I presented this for the first time at the Bristol maths conference in March 2019 which was a very scary moment for me!
To say that I was impressed with this method was an understatement. This process breaks the solving of linear equations down into small steps (atomisation).
The first step is known as “Decide” which is the most important step in the process (in my opinion). The decide steps are built up more and more as the linear equations become more advanced. I like to think of this as a bucket that is being filled more and more as students go through this mathematical journey.
We start this journey with expressions such as x+5 and ask the students “how do we get to x through addition or subtraction?”. Once they establish that they subtract 5 we can begin to make them more confident with expressions like x+2801 etc.

We then move on to solving equations of the form x+a=b. For example, solving the equation x+5=20. To do this, we ask students how we get to x from x+5. We subtract 5 so we BREAK the equation by doing x+5-5=20 and then REPAIR by doing x+5-5=20-5. We then SIMPLIFY to get x=15. We can continually build on this. To see how we can do this progressively, check out my powerpoint below!

